Identidades trigonométricas
Genaro Luna Carreto
Sin duda se ha encontrado un sinnúmero de identidades trigonométricas en todos sus cursos de matemáticas, pero ¿de dónde salieron?
Esta página tiene la finalidad de obtener algunas identidades trigonométricas importantes, a partir de: \begin{align} \sin^2 x + \cos^2 x &= 1 \tag{I}\label{I}\\ \sin (-x) &= -\sin x \tag{II}\label{II}\\ \cos (-x ) &= \cos x \tag{III}\label{III}\\ \sin (x+y) &=\sin x\cos y+\sin y\cos x \tag{IV}\label{IV} \end{align} Antes de empezar, un recordatorio.
DEFINICIÓN SENO Y COSENO
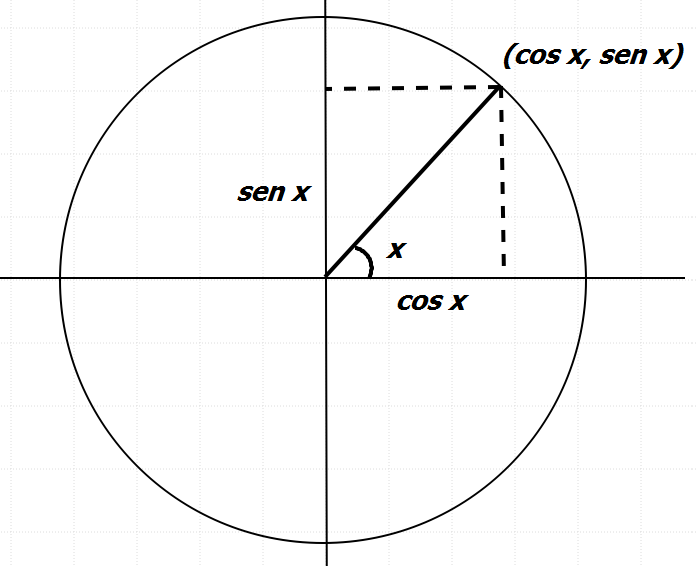 MODELO I : Las funciones trigonométricas $\sin $ y $\cos$ son definidas a partir de un círculo unitario. El $\cos x$ y $\sin x$, son las coordenadas
del punto sobre la circunferencia resultantes de la intersección el segmento, que sale del origen y forma una ángulo de magnitud $x$ (radianes) con el eje positivo de $X$.
Es inmediata entonces la llamada identidad pitagórica
\begin{align*}
\sin ^2 x + \cos^2 x=1
\end{align*}
Por otro lado si grafica el ángulo $-x$, obtendrá que
\begin{align*}
\sin (-x) &= -\sin x \\
\cos (-x) &= \cos x
\end{align*}
Si $x=0$, entonces el segmento queda sobre el eje horizoltal, por lo que $\cos 0=1$ y $\sin 0=0$. Con éste modelo y
recordando que $\frac{\pi}{2}$ equivale a 90º, ¿cuanto sería $\cos (\frac{\pi}{2})$?
MODELO I : Las funciones trigonométricas $\sin $ y $\cos$ son definidas a partir de un círculo unitario. El $\cos x$ y $\sin x$, son las coordenadas
del punto sobre la circunferencia resultantes de la intersección el segmento, que sale del origen y forma una ángulo de magnitud $x$ (radianes) con el eje positivo de $X$.
Es inmediata entonces la llamada identidad pitagórica
\begin{align*}
\sin ^2 x + \cos^2 x=1
\end{align*}
Por otro lado si grafica el ángulo $-x$, obtendrá que
\begin{align*}
\sin (-x) &= -\sin x \\
\cos (-x) &= \cos x
\end{align*}
Si $x=0$, entonces el segmento queda sobre el eje horizoltal, por lo que $\cos 0=1$ y $\sin 0=0$. Con éste modelo y
recordando que $\frac{\pi}{2}$ equivale a 90º, ¿cuanto sería $\cos (\frac{\pi}{2})$?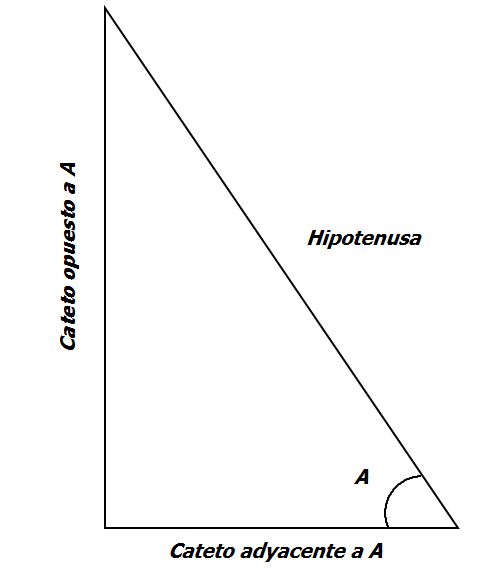
MODELO II : Este otro modelo referente a las funciones trigonométricas, se basa en los cocientes de las longitudes de los lados de un triángulo rectángulo. \begin{align*} \sin A &= \frac{\textrm{Cateto opuesto a A}}{\textrm{Hipotenusa}} \\ \cos A &= \frac{\textrm{Cateto adyacente a A}}{\textrm{Hipotenusa}} \\ \end{align*}
En base a éstas, se definen otras funciones: \begin{align*} \tan A&= \frac{\sin A}{\cos A}\\ \sec A&= \frac{1}{\cos A}\\ \end{align*} Además \begin{align*} \csc A &= \frac{1}{\sin A}\\ \cot A &= \frac{1}{\tan A} \end{align*} Aquí la identidad pitagórica es consecuencia del teorma de pitágoras.
La educación media y media superior usa por defecto éste último modelo.
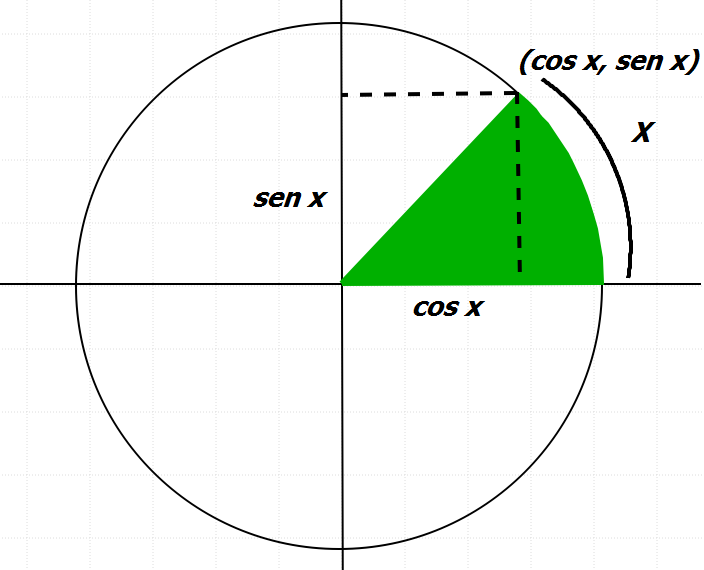
MODELO III : Ahora bien, la riqueza en propiedades de las funciones trigonométricas es extensa y con tales definiciones es imposible formalizarlas. Por ende, fue necesario visulizarlas de otra manera. La otra definición también se basa en un círculo unitario. Si $x$ es un número, los valores asignados a $\sin x$ y $\cos x$ son las coordenadas del punto sobre la circunferencia que determina un sector cuya área (teñida de verde) es $\frac{x}{2}$. Casualmente, bajo estas condiciones, el arco sobre la circunferencia determinado por el area verde mide $x$. La ventaja del modelo, radica en que, el área verde se puede poner como una función $A(x)$.
 Es notable la dificultad resultante. La formalidad a través de la cual
se trabaja la función área $A(x)$, conlleva el uso de herramienta matemática especializada: derivadas e integrales.
Sin embargo, con relativa facilidad, se logra obtener sus derivadas:
\begin{align*}
(\sin x)' &=\cos x\\
(\cos x)' &= -\sin x\\
\end{align*}
Con esta teoría y depués de un arduo proceso se obtiene la identidad
$$\sin (x+y)=\sin x\cos y+\sin y\cos x. \nonumber$$
Es notable la dificultad resultante. La formalidad a través de la cual
se trabaja la función área $A(x)$, conlleva el uso de herramienta matemática especializada: derivadas e integrales.
Sin embargo, con relativa facilidad, se logra obtener sus derivadas:
\begin{align*}
(\sin x)' &=\cos x\\
(\cos x)' &= -\sin x\\
\end{align*}
Con esta teoría y depués de un arduo proceso se obtiene la identidad
$$\sin (x+y)=\sin x\cos y+\sin y\cos x. \nonumber$$
Los tres modelos aportan elementos para la obtención de las identidades. El modelo III construye \eqref{IV} "limpiamente". Algunos libros, por ejemplo usan ésta para obtener la derivada del $\sin x$, pero no nos dicen como obtener \eqref{IV}.
Si quieres saber más sobre:
MODELO I : Leithold Louis, El Cálculo (7ª ed), Oxford University Press, México, 1998.
MODELO II : Cualquier libro de trigonometría te servirá.
MODELO III : Spivak Michael, Cálculo Infinitesimal(2ª ed), Reverté, México, 1996.
A continuación aparece una tabla con identidades trigonométricas que viene en la parte final de cualquier libro de ciencias exactas. Si quieres descargarla en formato pdf
aquí.
| IDENTIDADES TRIGONOMÉTRICAS (Genaro Luna Carreto) | ||
| $\sin ^2 x+\cos ^2x=1$ | $1+\tan ^2 x=\sec ^2 x$ | $1+\cot ^2 x=\csc ^2 x$ |
| $\sin (-x)=-\sin x$ | $\cos (-x)= \cos x$ | $\tan (-x)= -\tan x$ |
| $\cos (2\pi k + x)= \cos x$ | $\sin (2\pi k + x)=\sin x $ | $\displaystyle \tan x=\frac{\sin x}{\cos x}$ |
| $\displaystyle \sec x =\frac{1}{\cos x}$ | $\displaystyle \csc x =\frac{1}{\sin x}$ | $\displaystyle \cot x=\frac{1}{\tan x}$ |
| $\sin (x+y)=\sin x\cos y+\sin y\cos x$ | $\sin (x-y)=\sin x\cos y-\sin y\cos x$ | $cos(x+y)=\cos x \cos y-\sin x\sin y$ |
| $\cos (x-y)=\cos x \cos y+\sin x\sin y$ | $\displaystyle \tan (x+y)= \frac{\tan x +\tan y}{1-\tan x \tan y}$ | $\displaystyle \tan (x-y)= \frac{\tan x -\tan y}{1+\tan x\tan y}$ |
| $\sin 2x= 2\sin x \cos x$ | \begin{align*} \sin mx \cos nx =\frac{1}{2} \bigg[ \sin(m-n)x + \sin(m+n)x \bigg] \end{align*} | $\displaystyle \sin ^2 x= \frac{1-\cos 2x}{2}$ |
| $\displaystyle \cos ^2 x= \frac{1+ \cos 2x}{2}$ | \begin{align*} \sin mx \sin nx =\frac{1}{2} \bigg[ \cos(m-n)x - \cos(m+n)x \bigg] \end{align*} | $\cos 2x= \cos ^2x-\sin ^2x$ |
| \begin{align*} \cos mx \cos nx =\frac{1}{2} \bigg[ \cos(m-n)x + \cos(m+n)x \bigg] \end{align*} | ||
| \begin{align*} arc\tan x + arc\tan y = arc\tan \bigg[ \frac{x+y}{1-xy} \bigg] \end{align*} | ||
| \begin{align*} arc\sin x + arc\sin y = arc\sin \bigg[ x\sqrt{1-y^2} + y\sqrt{1-x^2}\bigg] \end{align*} | ||
Ahora presentamos la obtención de algunas identidades.
\begin{align} \label{sendoble}
\sin 2x= 2\sin x \cos x
\end{align}
SOLUCIÓN
Es sencilla, solo en \eqref{IV}, en lugar de $y$ coloque $x$ \begin{align} \sin (x+y) &= \sin x\cos y+\sin y\cos x \\ \sin (x+x) &= \sin x\cos x+\sin x\cos x \\ \sin 2x &= 2 \sin x\cos x \end{align}
SOLUCIÓN
Es sencilla, solo en \eqref{IV}, en lugar de $y$ coloque $x$ \begin{align} \sin (x+y) &= \sin x\cos y+\sin y\cos x \\ \sin (x+x) &= \sin x\cos x+\sin x\cos x \\ \sin 2x &= 2 \sin x\cos x \end{align}
\begin{align}\label{senresta} \sin (x-y)=\sin x\cos y-\sin y\cos x \end{align}
SOLUCIÓN
\begin{align*} \sin (x-y) &=\sin (x+(-y)) = \sin x\cos (-y)+\sin (-y)\cos x\\ &=\sin x\cos y-\sin y\cos x\\ &=\sin x \cos y -\sin y \cos x\\ \end{align*}
\begin{align} \label{cossuma} cos(x+y)=\cos x \cos y-\sin x\sin y \end{align}
SOLUCIÓN
Se utiliza \eqref{IV}. Se tiene que considerar una de las dos variables, $x$ ó $y$ como constantes y derivar. Yo tomaré a $y$ como constante. Asi que derivaré $\sin(x+y)$, con respecto a $x$. \begin{align} \bigg[ \sin(x+y) \bigg]' &= \bigg[ \sin x\cos y+\sin y\cos x \bigg]' \\ &= \cos x \cos y + \sin y (-\sin x)\\ &=\cos x \cos y - \sin y \sin x \end{align} Por otro lado $$\bigg[ \sin(x+y) \bigg]'= \cos (x+y),$$ por lo tanto $$\cos (x+y)=\cos x \cos y - \sin y \sin x$$
\begin{align}\label{cosdoble}
\cos 2x= \cos ^2x-\sin ^2x
\end{align}
SOLUCIÓN
Es una consecuencia de la identidad \eqref{cossuma}. Si $y=x$ en \eqref{cossuma} \begin{align*} \cos (x+y) &=\cos x \cos y - \sin y \sin x \\ \cos (x+x) &=\cos x \cos x - \sin x \sin x \\ \cos 2x &=\cos ^2 x - \sin^ 2 x \\ \end{align*}
SOLUCIÓN
Es una consecuencia de la identidad \eqref{cossuma}. Si $y=x$ en \eqref{cossuma} \begin{align*} \cos (x+y) &=\cos x \cos y - \sin y \sin x \\ \cos (x+x) &=\cos x \cos x - \sin x \sin x \\ \cos 2x &=\cos ^2 x - \sin^ 2 x \\ \end{align*}
\begin{align}
\sin ^2 x= \frac{1-\cos 2x}{2}
\end{align}
SOLUCIÓN
Despejando $\cos^2 x$ en la identidad pitagórica \eqref{I}, resulta que $\cos^2 x=1- \sin ^2 x$. Ahora sustituya $\cos^2 x$ en la identidad \eqref{cosdoble} \begin{align} \cos 2x &=\cos ^2 x - \sin^ 2 x\\ &= 1- \sin^2 x - \sin^2 x \\ &=1-2\sin^2 x\\ \end{align} en consecuencia \begin{align} 1-2\sin^2 x &= \cos 2x \\ -2\sin^2 x &= -1+ \cos 2x \\ 2\sin^2 x &= 1- \cos 2x \\ \sin^2 x &= \frac{1- \cos 2x}{2} \end{align}
SOLUCIÓN
Despejando $\cos^2 x$ en la identidad pitagórica \eqref{I}, resulta que $\cos^2 x=1- \sin ^2 x$. Ahora sustituya $\cos^2 x$ en la identidad \eqref{cosdoble} \begin{align} \cos 2x &=\cos ^2 x - \sin^ 2 x\\ &= 1- \sin^2 x - \sin^2 x \\ &=1-2\sin^2 x\\ \end{align} en consecuencia \begin{align} 1-2\sin^2 x &= \cos 2x \\ -2\sin^2 x &= -1+ \cos 2x \\ 2\sin^2 x &= 1- \cos 2x \\ \sin^2 x &= \frac{1- \cos 2x}{2} \end{align}
\begin{equation}
\displaystyle \tan (x+y)= \frac{\tan x +\tan y}{1-\tan x \tan y}
\end{equation}
SOLUCIÓN
De la definición de tangente \begin{align*} \tan (x+y) &= \frac{\sin (x+y)}{\cos (x+y)} \\ \end{align*} Debido a \eqref{cossuma} y \eqref{IV} \begin{align*} \tan (x+y) &= \frac{\sin (x+y)}{\cos (x+y)} \\ &=\frac{\sin x\cos y+\sin y\cos x}{ \cos x \cos y - \sin y \sin x} &= \frac{\frac{\sin x\cos y+\sin y\cos x}{\cos x \cos y }}{ \frac{ \cos x \cos y - \sin y \sin x}{\cos x \cos y }} \\ &= \frac{ \frac{\sin x\cos y}{\cos x \cos y } + \frac{\sin y\cos x}{\cos x \cos y} }{ \frac{\cos x \cos y }{\cos x \cos y} - \frac{\sin y \sin x}{\cos x \cos y} } \\ &=\frac{\tan x +\tan y}{1-\tan x \tan y} \end{align*}
SOLUCIÓN
De la definición de tangente \begin{align*} \tan (x+y) &= \frac{\sin (x+y)}{\cos (x+y)} \\ \end{align*} Debido a \eqref{cossuma} y \eqref{IV} \begin{align*} \tan (x+y) &= \frac{\sin (x+y)}{\cos (x+y)} \\ &=\frac{\sin x\cos y+\sin y\cos x}{ \cos x \cos y - \sin y \sin x} &= \frac{\frac{\sin x\cos y+\sin y\cos x}{\cos x \cos y }}{ \frac{ \cos x \cos y - \sin y \sin x}{\cos x \cos y }} \\ &= \frac{ \frac{\sin x\cos y}{\cos x \cos y } + \frac{\sin y\cos x}{\cos x \cos y} }{ \frac{\cos x \cos y }{\cos x \cos y} - \frac{\sin y \sin x}{\cos x \cos y} } \\ &=\frac{\tan x +\tan y}{1-\tan x \tan y} \end{align*}
\begin{align*}
\sin mx \cos nx =\frac{1}{2} \bigg[ \sin(m-n)x + \sin(m+n)x \bigg]
\end{align*}
SOLUCIÓN
Una identidad que resulta de \eqref{senresta} y \eqref{IV}. \begin{align} \sin (m-n)x &= \sin (mx-nx)\\ &=\sin mx \cos nx - \sin nx \cos mx\\ \end{align} Por otro lado \begin{align} \sin (m+n)x &= \sin (mx+ nx)\\ &= \sin mx \cos nx + \sin nx \cos mx \end{align} A continuación sumanos \begin{align} \sin (m-n)x + \sin (m+n)x &= 2 \sin mx \cos nx \\ \end{align} Entonces \begin{align} \sin mx \cos nx &= \frac{1}{2} [ \sin (m-n)x + \sin (m+n)x ] \\ \end{align}
Una identidad que resulta de \eqref{senresta} y \eqref{IV}. \begin{align} \sin (m-n)x &= \sin (mx-nx)\\ &=\sin mx \cos nx - \sin nx \cos mx\\ \end{align} Por otro lado \begin{align} \sin (m+n)x &= \sin (mx+ nx)\\ &= \sin mx \cos nx + \sin nx \cos mx \end{align} A continuación sumanos \begin{align} \sin (m-n)x + \sin (m+n)x &= 2 \sin mx \cos nx \\ \end{align} Entonces \begin{align} \sin mx \cos nx &= \frac{1}{2} [ \sin (m-n)x + \sin (m+n)x ] \\ \end{align}
4-junio-2014